全国の小学生、中学生、高校生の諸君!席替えで座席位置に悩んだことはないかな?今回は早く帰りたいと願う同志に向けて自身の考察結果と座席位置の提案をしようと思う。
この記事で想定している読者
- 効率的な帰宅をしたいと考えている小学生、中学生、高校生の方
- 席替えで教室内の座席位置に悩んでいる方
教室内の座席位置の重要性
一般的に帰宅という言葉を聞くと、多くの人は学校から家までの通学ルートを想像し、ここを効率化することを考えるのではないかと思う。
甘い…甘すぎると言わざるを得ない。計算問題の答えを出して検算しない程度には甘い…。
帰宅とは朝の通学時からいつもと変わらない道路交通状況になっているか、その日の予定、帰宅予想時間、教室の座席位置等あらゆる要因を分析し、その日その日で最も効率的な帰宅を実現する必要がある。

ここで失敗すると、帰宅のスタートで大幅なロスが生じる他、先生や学友から特に(自身にとって)それほど重要でもない用事で呼び止められ、つまらない時間ロスを発生させる要因にもなる。
従って、帰宅の理想的なスタートを切るために教室の座席位置を考察しておくことは非常に重要なのである。
学校教室のレイアウト
まず、下の図3を見てほしい。これは私が小学生の頃に通っていた学校(1クラス35人)の教室のレイアウトと寸法を示したものである。
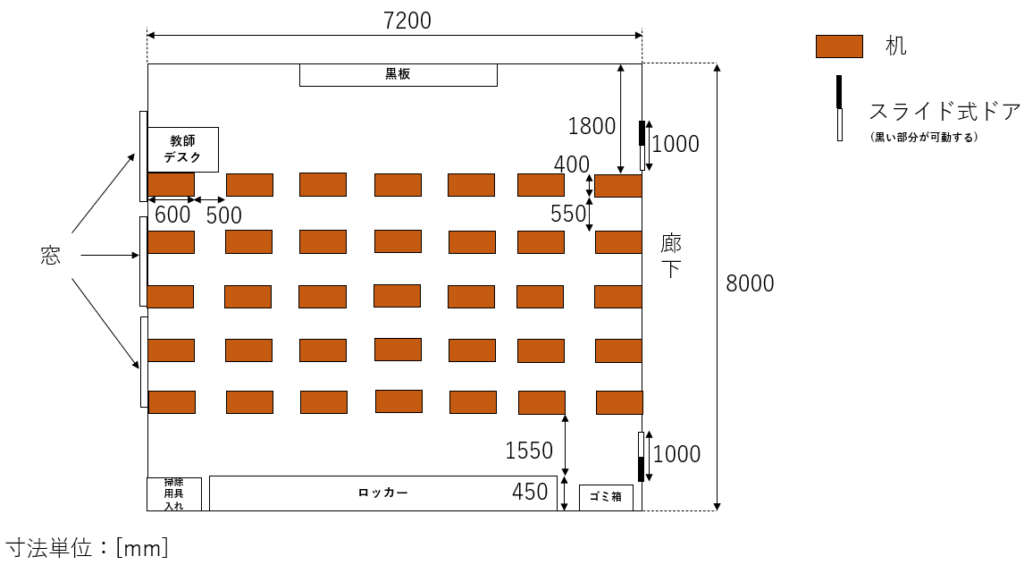
図3. 教室のレイアウトと凡その寸法
これは私が小学生の頃に物差しで測った情報を参考にまとめたものである。
文部科学省のHPによると、学校教室のサイズは昭和25年に、学校施設を全国一定レベルに整備できるよう、「鉄筋コンクリート造の標準設計」が作成された。これにより、教室の広さが奥行7m、間口が9mとなるよう多くの学校教室が整備されたとされている。
今回図3で示した教室の広さは上記の標準から若干異なっているが、机のレイアウトという面では大きく変わらないため、読者の皆様の帰宅検討をするうえではあまり大きな影響は受けないと考えている。(座席位置とドアの位置がわかり、教室脱出までの計算ができれば問題ないと考えられるため。)
なお、中学校、高校では教師デスクが教壇に代わり、教室の前方中央部に位置変更となることが多い。
座席位置提案
では、前項で示した教室レイアウトにおいて、効率的な帰宅が実現できる(理想的な)お勧め座席位置について紹介しよう。
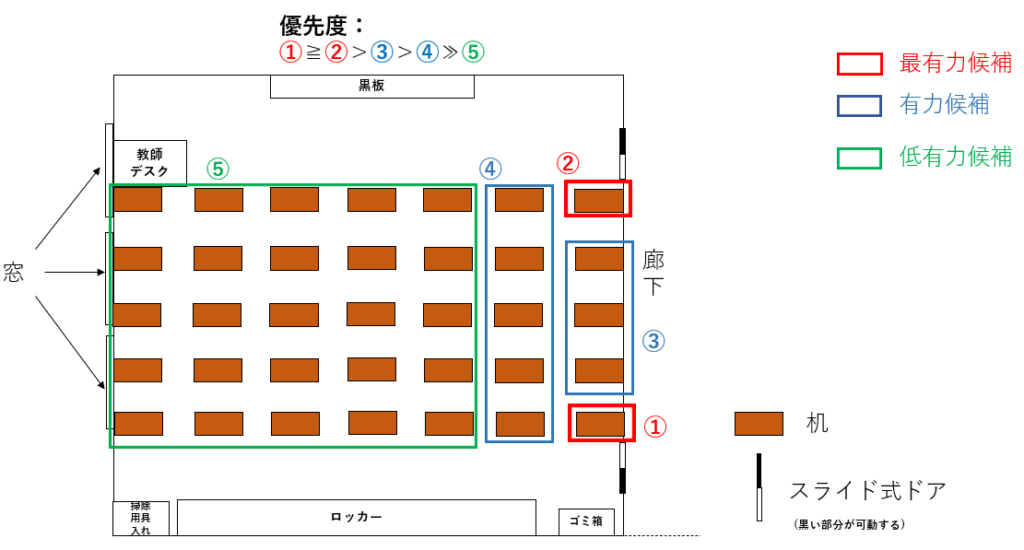
図4. お勧め座席位置
概要:
- ①、②は最もドアの位置に近いため、終礼後に最も早く教室から脱出できる。
- ③は①、②程ではないが比較的早くドアに到達できる。
- ④は③と比較した場合、そこまで大きな差は出ないと考える。但し、終礼後に人がドアに殺到するため、状況を見てどちらのドアから脱出した方が良いかを都度検討する必要がある。
- ⑤は終礼後、ドアまでの到達距離が長く、アクセスに時間がかかるためお勧めしない。
①と②のうち、どちらがお勧めなのかは一概には言えない。この帰宅ミッションは自宅まで如何にして早く帰れるかを検討している。
そのため、学校という視点で見るなら、どのようなルートで校門に出るかが重要になるため、校舎内における教室の位置や下駄箱の位置を考慮して帰宅ルートを検討する必要がある。これについては別記事にて解説する。
⑤についてだが、お勧めできない理由として下記の点が挙げられる。
- ドアに近い人がある程度教室の外に出ないと教室からは出られない。
- 窓側の人は教師デスクにも近く、教師から余計な仕事を放課後に依頼される可能性が高い。
これはキツイ…特に窓際の人は教室からの脱出時間という観点を考慮すると⑤の人たちは①、②の人たちと比べて大きな時間ロスを抱えることになると考えられる。
追加補足事項:
放課後帰宅を考える際に学校で実施される清掃活動を考慮に入れる必要がある。今まで学友や親戚、会社の同僚など様々な人から情報をかき集めたが、学校や地域によってこの教室の清掃活動をするタイミングややり方に違いがあるようだ。
例えば筆者の通っていた小学校、中学校、高校ではいずれも終礼後に全員が机を教室の後ろに下げてから帰宅する。(机を下げた後はあらかじめ決められた掃除当番が掃除をした後に机をもとに戻すような習慣があった。)
このとき、廊下側の机は教室後方のドアによる出入りを可能にするため、少し中央側に寄せて机を下げるのと、窓際の人は机の下げる位置は掃除用具が取り出せるように人一人分くらいのスペースを残して下げるようにしていた。
話を聞く限りでは、この掃除については昼休みが終わった後に掃除をする場合(終礼時は追加作業無しで即帰宅できる。)や、机を前方に寄せる学校もあるようだ。
但し、以降の考察を進めるうえではいったん筆者の学校で実施していた終礼後に机を後ろに下げるという前提で終礼後の教室からの脱出について考察を進める。
なぜ、ドア付近の座席位置が重要なのか?
前章でも少し触れたが、ドア付近の座席位置①,②を提案しているのは、最も早い時間で教室から脱出できるからである。
この脱出には以下の要素を考慮する必要があるが、ドア付近の座席位置はいずれも最速で脱出するという点において有利であると筆者は考えている。
- 机の移動を完了させる時間
- 机の移動完了後、ドアまでの距離
- 先生に見つかりやすい場所
教室内の移動時間はその人の歩く速度や教室内の混み具合も考慮する必要がある。
そのため、考察を簡単にするためにこの記事では学生が教室を出るまでに移動する距離に着目して考察を進める。
机の移動完了時間は、移動させる距離に大きく依存している。また、後ろに人がいる場合、その人が机を移動させ終わり、教室から脱出しないと次の人が教室から脱出できない。
この点を考慮すると廊下側最後尾の座席位置の人は一番早く自由に移動ができるようになる。
次にドアまでの距離だが、これは純粋にドアに近い列の人ほど有利だ。人の移動の速さを一定とするなら、ドアに最も近い座席位置の人が最も早くドアに到達するからである。
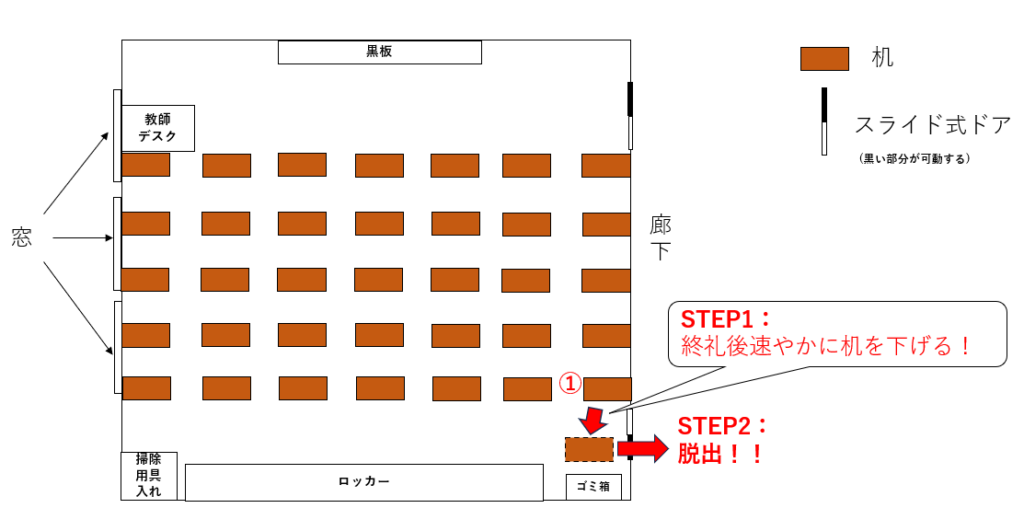
図5-1. ①の座席位置の人が教室を出るまでの流れ
一方、廊下側の座席にいる③のエリアにいる人は①の人の動きを見て、前方のドアから出た方が早いのか、後方ドアから出た方が早いのかを判断すればよい。
では、②の座席位置にいる人はどのような行動選択をすべきか?
これは①の位置とは少し戦略が異なる。(③のエリアにいる人たちの対応に強く影響を受けるからだ。)具体的には、机を後方に下げた後にドア付近の込み具合を考慮して下図のSTEP2-1またはSTEP2-2を選択する必要がある。
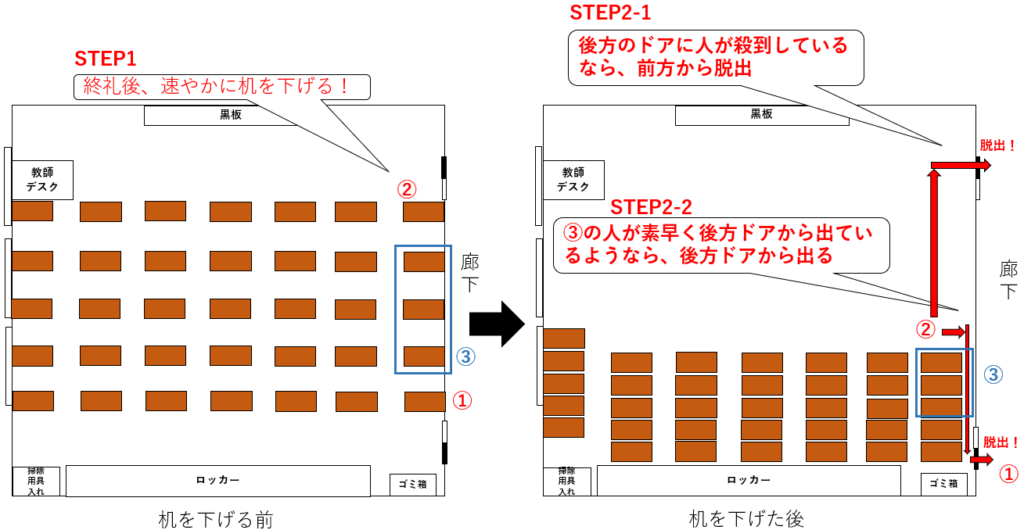
図5-2. ②の座席位置の人が教室を出るまでの流れ
最後に④、⑤のエリアの人たちの動きを確認しよう。
④、⑤の人はいずれも基本的に前方ドアからの脱出を優先的に検討すべきである。後方ドアは通路が狭く人がなかなか出られないため、結果として前方ドアから出た方が得なことが多い。
但し、①、③(場合によっては②も含めて)が優れた移動能力と状況判断能力を持っている学生であるなら④のエリア前方の人までは後方ドアからの脱出を検討してもよいかもしれない。
⑤はいわゆる教室脱出における第2陣に相当する位置の人たちである。机を下げた時点では既に後方ドアは人であふれているので、なるべく早く前方ドアから出られるように動くしかないと考えられる。
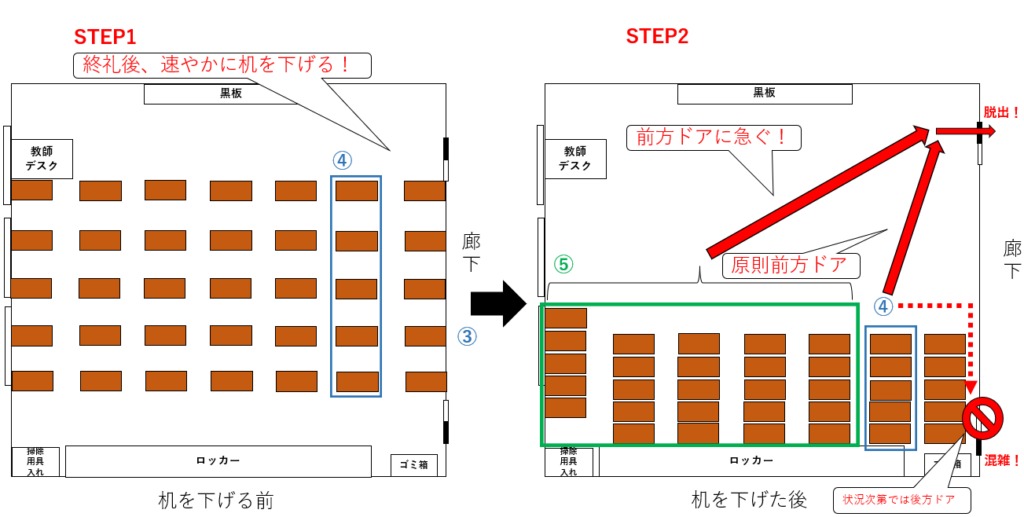
図5-3. ④、⑤のエリアの座席位置の人が教室を出るまでの流れ
ドア付近の座席①、②の脱出距離考察
この章では机を後方に移動させるという前提の元、座席位置①と②とでどの程度ドアへの到達時間に差が出るのかを考える。
考察の前提:
・今回の考察で使用する机は下記の規格のものを用いるとする。
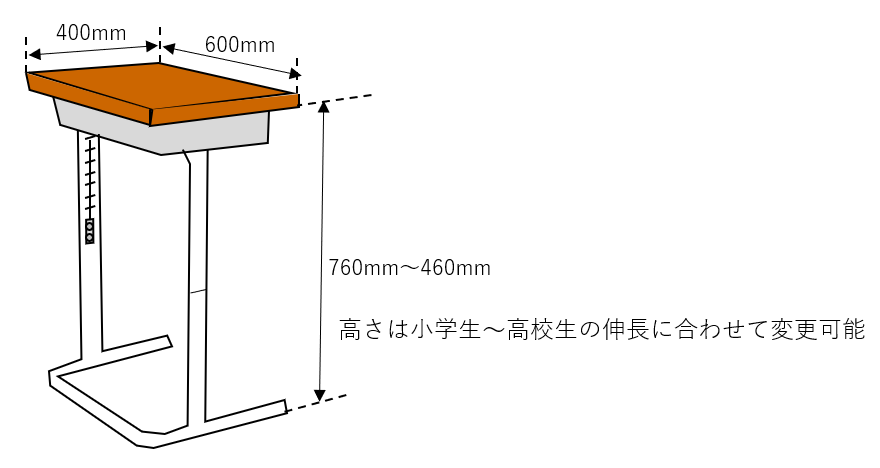
図6-1. 机の外観サンプル (詳細な規格は「タナベ事務機器様HP」を参照。)
・後方・前方のドアは可動式で、下図の黒い部分が可動部であるとする。
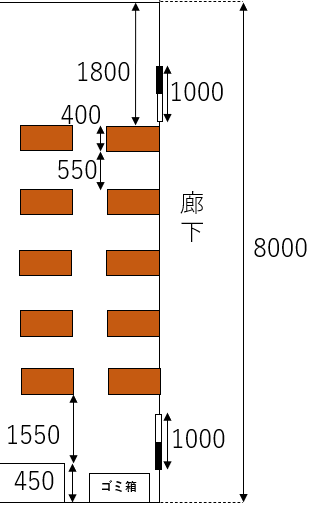
図6-2. 教室の廊下側拡大図
・最後尾の机は後方に1550mm下げるとする。
では、まず①の座席位置にいる人が終礼後、教室を出るまでに移動する距離を確認していこう!
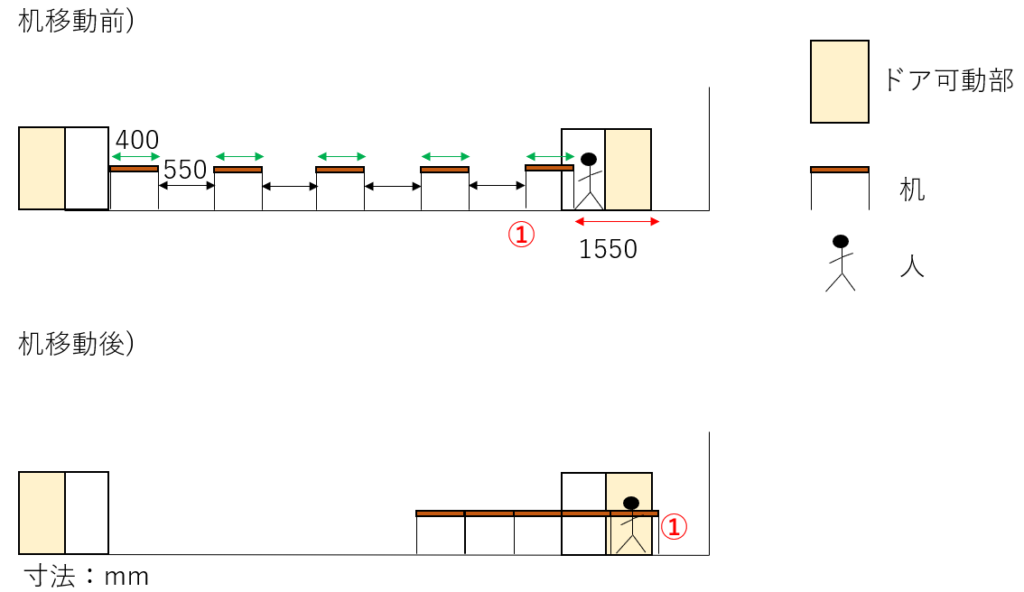
図6-3. ①の人が机を下げてから後方ドアを出るまでに移動した距離
上図6-3より、①の座席位置の人は机を後方に1550mm移動後、ドアを出るだけ。
よって①の人の移動距離は1550mmとなる。
次に②の座席位置にいる人が教室を出るまでの移動距離を考える。なお、②の人については後方ドアから出る場合と前方ドアから出る場合の2通りを考える。
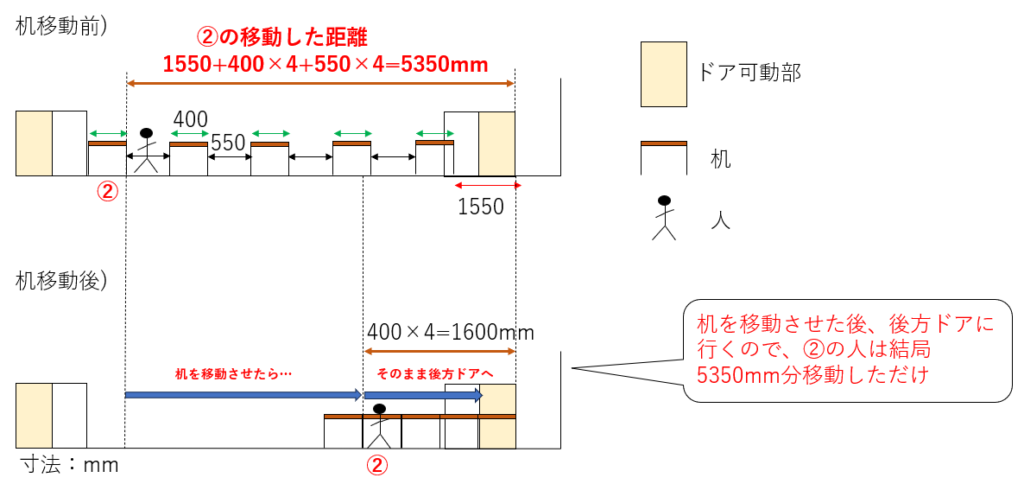
図6-4. ②の人が机を下げてから後方ドアを出るまでに移動した距離
これは簡単だ!上図6-4の通り、②の人は終礼後に机を5350mm分下げるが、そのまま後方ドアに行くので、結局②の移動距離は元の机の位置から後方ドアまでの距離に等しくなる。
よって移動距離は5350mmだ。
次に②の人が前方ドアを使って教室を出る場合を考える。
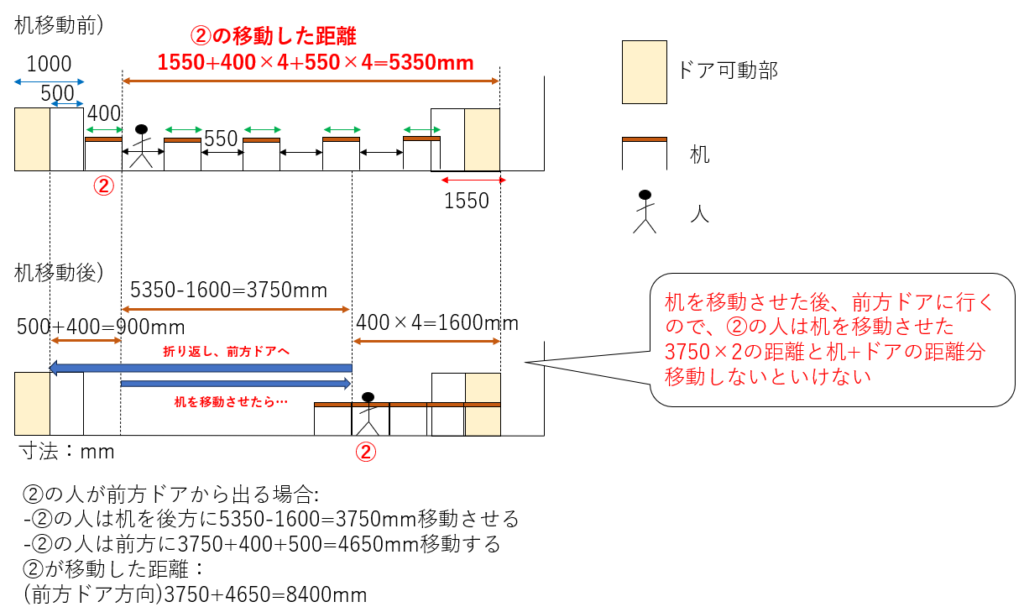
図6-5. ②の人が机を下げてから前方ドアを出るまでに移動した距離
これは少し複雑だ。②の人の動きに着目すると、最初に机を後方に3750mm下げる。その後、前方ドアに向かうので、元の机の位置までは戻らないといけない。さらにそこから机分の長さ400mmとドアの幅の半分(ドアの可動部に至るまでの距離=1000÷2=500mm)の距離をさらに移動する必要がある。
よって、②の人が最終的に前方ドアに到達するまでに移動する距離は下記のようになる。
合計移動距離=(机を移動した距離の往復分)+(机の幅)+(可動式ドアの距離の半分)
これを具体的な数値にして計算すると、図6-5のように8400mm分移動する必要があるとわかる。以上をまとめると以下の表6-1のようになる。
表6-1. 座席位置①と②の人が教室を出るまでに必要となる移動距離
| 座席位置①の人 | 座席位置②の人 | ||
| 後方ドアから出る場合 | 前方ドアから出る場合 | ||
| 移動距離[mm] | 1550 | 5350 | 8400 |
| ①の人との距離比較 | N/A | 3.45倍 | 5.41倍 |
上の表からもわかる通り、①、②共に後方ドアから出る場合で比較すると②は①の約3.45倍も移動しなければならない。
さらに、②が前方ドアから出る場合を考えると、②は①と比較して約5.41倍も長い距離を移動しなければならない。
実際にはこの距離に加えて、③のエリアにいる学生の立ち位置や動きを考慮する必要がある。
この結果を見れば①のポジションが教室の脱出という点において如何に効率的かがお分かり頂けたと思う。
ドアから最も遠い席と最も近い席の人との脱出距離比較
参考までに、ドアから最も遠くなる座席位置(下図7-1における⑤-1と記載した場所)と①の座席位置における移動距離の比較検討をしてみよう!
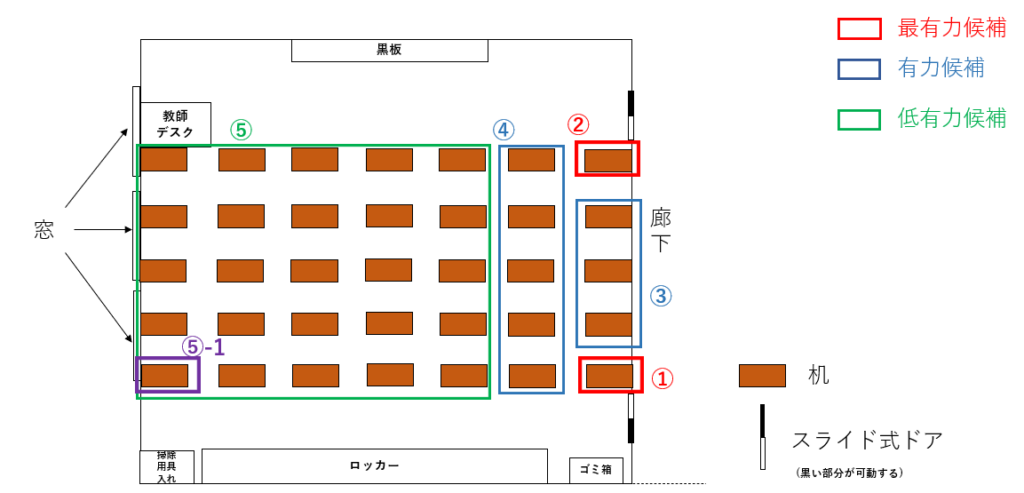
図7-1. ドアから最も遠い座席位置
この⑤-1に相当する座席位置の人は終礼後、以下のような手順で教室から出ることになる。
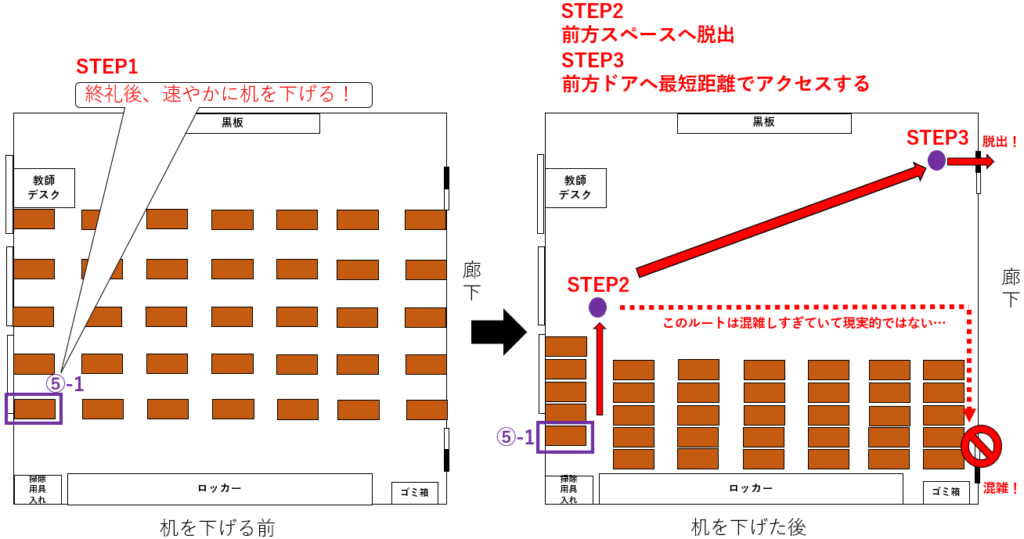
図7-2. ⑤-1の人が教室を出るまでの理想的なルート
上図7-1の通り、⑤-1は机を下げた(STEP1)後、まず教室の前方スペースへ出る(STEP2)必要がある。この後は、他の生徒の動き次第ではあるものの、理想的には前方ドアへ最短距離で直進(STEP3)し、教室を脱出するという流れになる。
但し、この座席位置のひとはもうひとつ考慮しなければならないことがある。
それは…掃除当番の人である!!
机を下げた後、掃除当番の人は⑤-1の後方にあるロッカーから掃除用具をとるために集まってくるのである。⑤-1のひとは速やかに机を下げてSTEP2の位置に進めないと、この掃除当番の人の流れに逆らって教室前方へ出る必要があるため大幅な時間ロスにつながる…。
では、以下の条件で⑤-1の人が前方ドアを脱出するまで移動する距離を検討していく。
- 検討を簡略化するため、本検討において他の生徒の動きは考慮しない。
- ⑤-1は後方に机を1000mm移動させるものとする。
- 図7-2のSTEP2~STEP3への移動は直線距離を移動するものとする。
- 前方ドアの可動部分は教室前方から計測して1300mm(=1800-500)の位置にあるとする。
まず、図7-2のSTEP1,2を図示すると下図7-3のようになる。
では、以下の条件で⑤-1の人が前方ドアを脱出するまで移動する距離を検討していく。
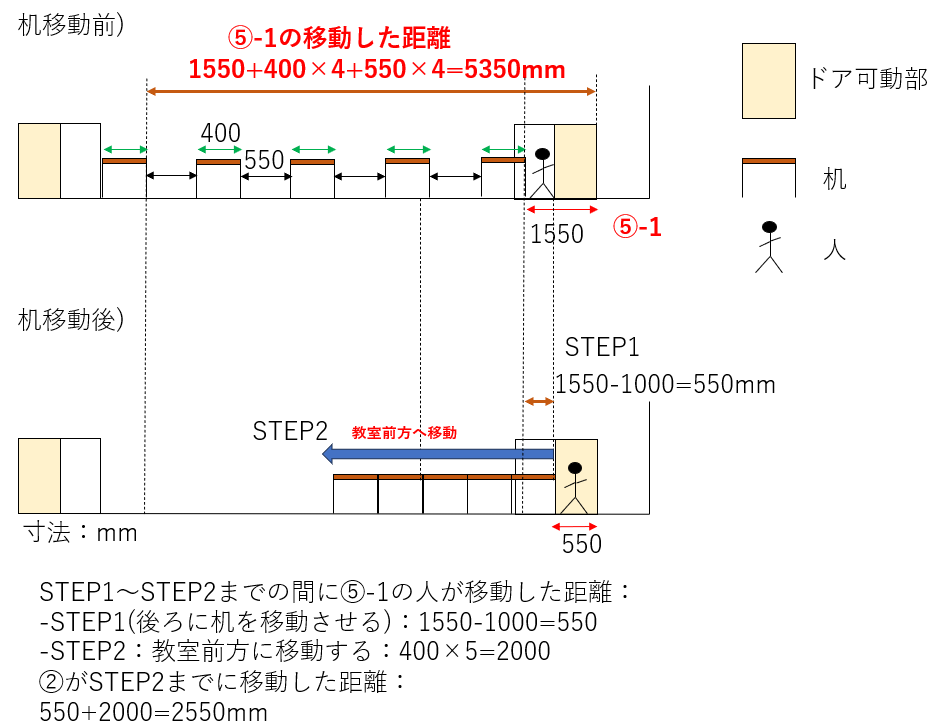
図7-3. STEP1,2における⑤-1の移動
次に⑤-1の人がSTEP2~3へ移動する距離を計算していこう。
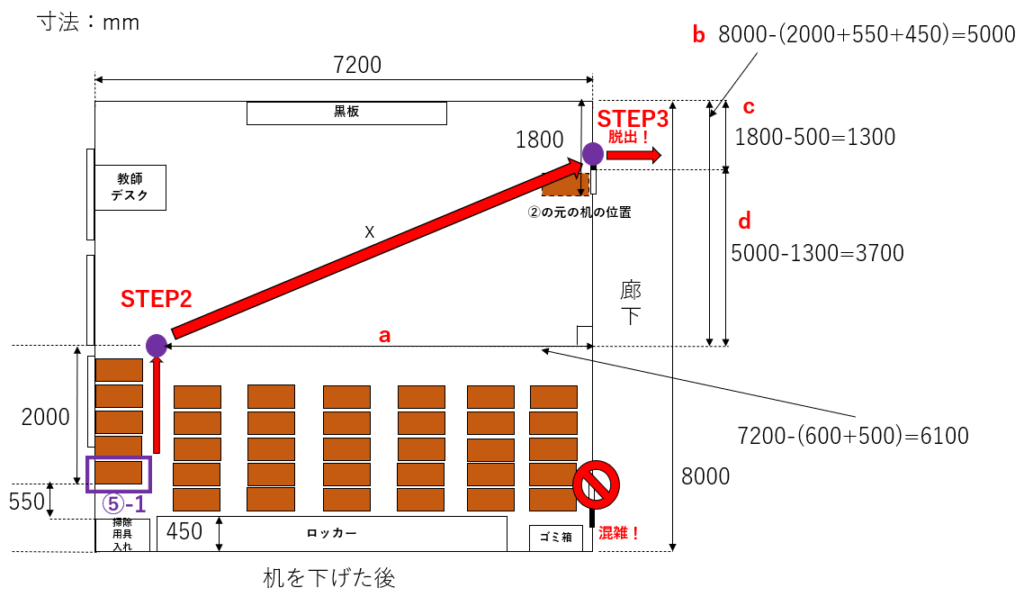
図7-4. STEP2,3における⑤-1の移動
図7-4のxを求める必要がある。ややこしいので図中のa~dの値をまずは算出しよう。
まず、aだが、教室の横の長さ全体から机と通路一つ分の距離を引けばよい。よって図3も考慮して以下の式が成り立つ。
\[a=8000-(2000+550+450)=6100\]
次にbを求めてみよう。bは図7-3で計算した⑤-1の移動距離を教室の縦の長さ全体から引けばよい。よって、図3も考慮して以下の式が成り立つ。
\[b=7200-(600+500)=5000\]
cは図3で示した教室前方のスペース1800mmからドアの大きさの半分(500mm)を引いた値である。よって以下のような式で求まる。
\[c=1800-500=1300\]
最後にdだが、これはbからcを引けばよい。
\[d=b-c=5000-1300=3700\]
以上の式を用いると、求める値xは三平方の定理より
\[x=\sqrt{a^2+d^2}=\sqrt{6100^2+3700^2} \fallingdotseq 7134\]
となる。
よって座席位置⑤-1の移動距離Lは以下のようになる。
\[L=2550+7134=9684\]
以上の考察をまとめると以下の表7-1のようになる。
表7-1. 座席位置①、②、⑤-1の人が教室を出るまでに必要となる移動距離
| 座席位置①の人 | 座席位置②の人 | 座席位置⑤-1の人 | ||
| 後方ドアから 出る場合 | 前方ドアから 出る場合 | |||
| 移動距離[mm] | 1550 | 5350 | 8400 | 9684 |
| ①の人との距離比較 | N/A | 3.45倍 | 5.41倍 | 6.24倍 |
実際には上記の理論距離に加え、他の生徒の移動を考慮する必要がある。これらを踏まえると、座席位置①の人と、最もドアからの距離が遠い⑤-1の人との間にできる教室を出るまでの時間は途方もない差になって表れてくる。
理想的な座席を狙うための戦略
では我々はどのようにして理想的な座席位置を狙うべきか?
確かに筆者は図4で示した座席位置と優先度に従って席替えのくじ引きやじゃんけんに臨むことを提案した。
しかしながら、現実問題として座席位置①を狙うのはかなり難しい。35人でくじ引きをするにしても全員が同時にくじを引くなら確率は\( \frac{1}{35} \)である。
実際には順番にくじを引くのでもう少し確率は大きくなるが…大した差は出ない…。
そのため、最速ではないものの、安定して帰宅時間を縮めるために下記の座席位置を狙うことを改めて提案する。
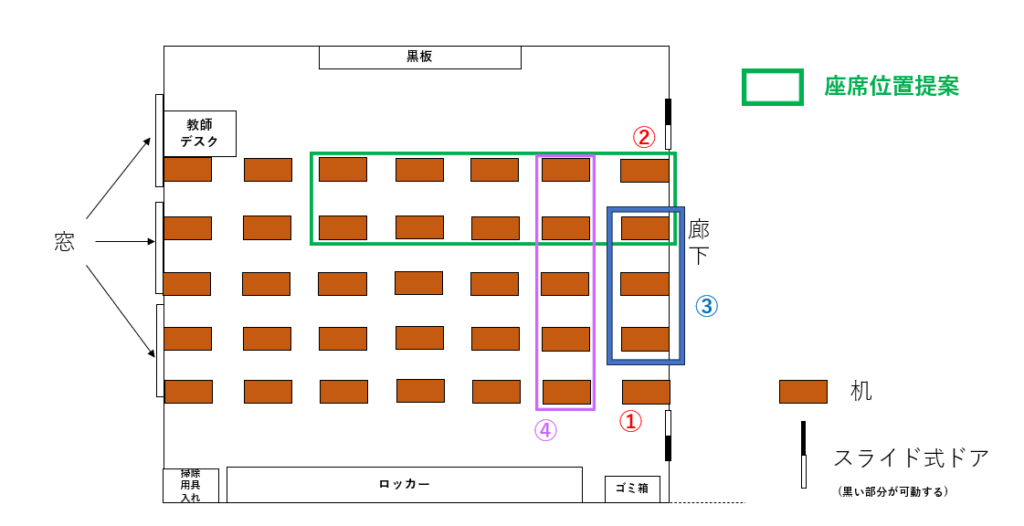
図8. 座席位置提案
この図8で示したエリアであればくじで希望の座席エリアを狙いやすくなる。加えて、教室前方のエリアに至っては、「後ろだと文字が見えにくい」という理由をつけて前の席を優先的に狙うことも可能だ。
確かに①を狙えるのが理想だが、ピンポイントで希望を通すのはなかなか難しいと思われる。③、④のエリアも同様である。
加えて、終礼時は教師が教室前方中央部に立つことが多い。この時、教室両端最前列が視界の端に位置するため、見つかりにくい。
放課後、教師から雑用を依頼されることがたまにあるが、こうした視界の端に位置する生徒は依頼されづらいと筆者は考えている。
まとめ
この記事では教室を出るという観点で、どの座席が最も早く教室を出られるのかに考察した。
終礼後、掃除のために机を教室後方部に移動させるという前提をおいた結果、図8の①が最も効率的であるという結果を示しました。
但し、毎回席替えの時にピンポイントで特定の座席を狙うのは現実的ではないため、ある程度の妥協は必要だと思う。
大切なのは、door to doorの帰宅効率性であり、教室から脱出する速さだけがすべてではないということです。帰宅ルート全体を考えて妥協できるところとそうでないところを切り分けるとよいでしょう。
また、地域によっては終礼後に机を移動させない、前方に移動させるなどの違いが出ると思います。
そうした事情を踏まえてこの記事の考察を応用すれば同じように効率的な座席位置の特定はできると思う。
最後に、教室や座席位置の寸法は小学校のものを参考にしてはいるが、中学校、高校においてもそこまで大きくは変わらないと考える。
万が一規格が大きく異なっていたとしても、この記事で紹介した方法と同様のアプローチで計測と考察が可能だ。
この考察が読者の皆様の帰宅検討の一助になれば幸いです。


